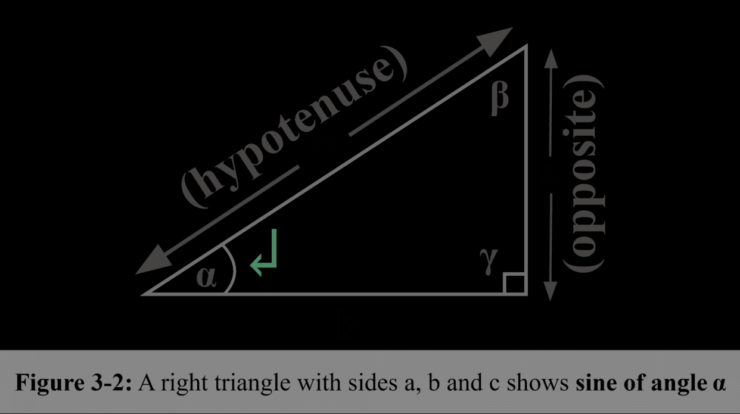
Sine definition – The sine function, a cornerstone of trigonometry, is a mathematical tool with far-reaching applications in diverse fields. From its inception as a geometric concept to its modern-day usage in computer graphics, sine has played a pivotal role in shaping our understanding of the world.
Delving into the depths of sine definition, we embark on a journey that unravels its mathematical essence, trigonometric underpinnings, graphical characteristics, and practical applications.
Definition and Overview
The sine function is a mathematical function that describes the vertical component of a point moving in a circular motion. It is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right triangle.
Sine is used in a wide variety of applications, including:
- Navigation
- Trigonometry
- Sound and music
- Computer graphics
Trigonometric Circle and Unit Circle
The trigonometric circle is a circle with radius 1 that is used to define the sine function. The unit circle is a trigonometric circle that is centered at the origin.
The sine of an angle is equal to the y-coordinate of the point on the unit circle that corresponds to that angle.
Sine Function Graph
The graph of the sine function is a periodic function that repeats every 2π units. The graph has a maximum value of 1 and a minimum value of -1.
The key features of the sine function graph are:
- Amplitude: 1
- Period: 2π
- Symmetry: Odd
Applications in Calculus
The sine function is used in calculus to find the derivatives and integrals of functions.
For example, the derivative of the sine function is the cosine function.
Applications in Physics and Engineering
The sine function is used in physics and engineering to study sound, light, and other physical phenomena.
For example, the sine function is used to describe the motion of a pendulum.
Applications in Computer Graphics
The sine function is used in computer graphics to create realistic images and animations.
For example, the sine function is used to create the illusion of movement in video games.
Inverse Sine Function, Sine definition
The inverse sine function (arcsine) is the function that returns the angle whose sine is equal to a given value.
The inverse sine function is used in a variety of applications, including:
- Solving equations
- Finding the angle of incidence of a light ray
Epilogue: Sine Definition
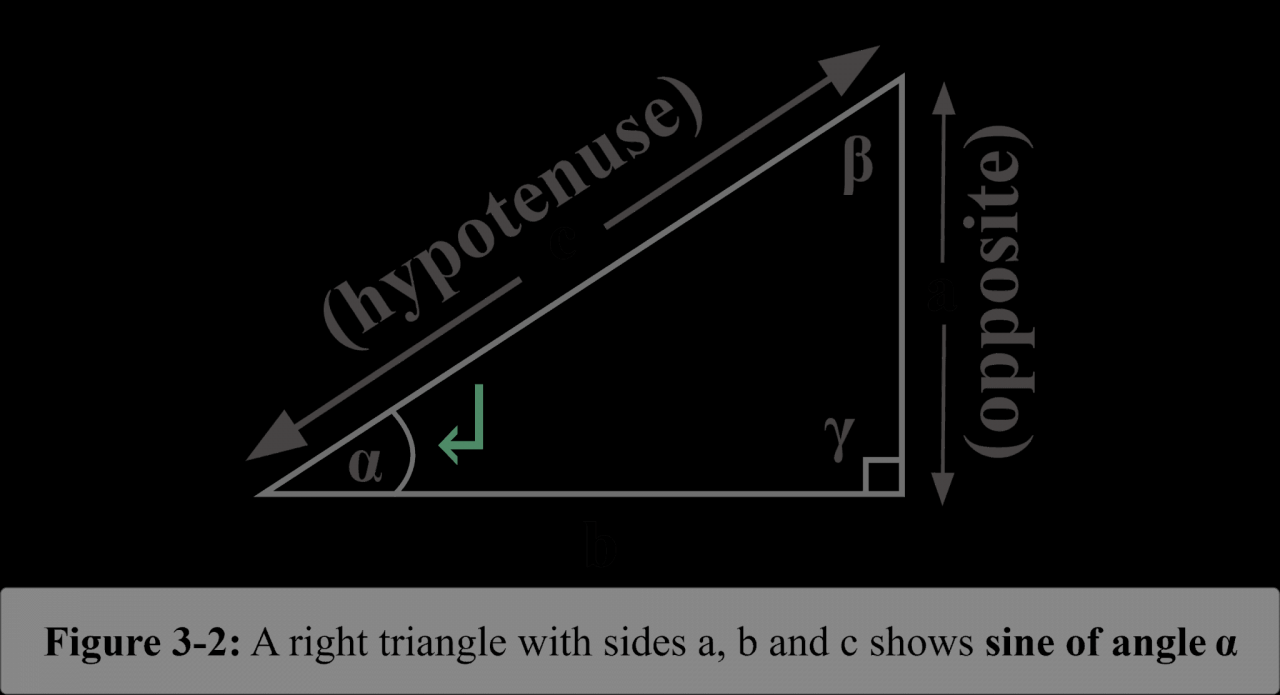
In conclusion, the sine function stands as a testament to the power of mathematics to describe and predict the intricacies of our world. Its versatility and ubiquity make it an indispensable tool for scientists, engineers, and artists alike, empowering them to push the boundaries of knowledge and innovation.
Questions and Answers
What is the mathematical definition of sine?
Sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle.
How is sine used in real-world applications?
Sine is used in various fields, including navigation, sound engineering, and computer graphics, to solve problems involving angles and periodic phenomena.